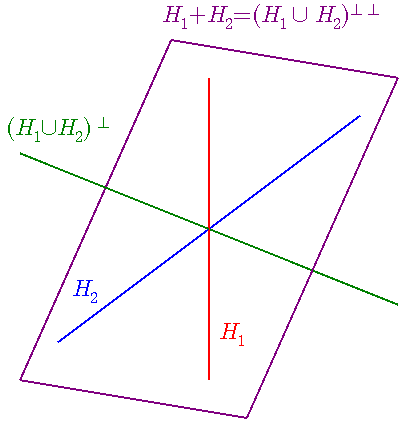
上限 H1 ∨ H2 のイメージ図
上図では H1 と H2 は ともに 3 次元 Euclid 空間 ℝ3 における 1 次元線形部分空間.
(H1 ∪ H2)⊥ は H1 と H2 に垂直な 1 次元線形部分空間となり,
その直交補空間が (H1 ∪ H2)⊥⊥ であり, これは H1 + H2 に等しい.
そして,これが {H1, H2} の上限 H1 ∨ H2 である.
G = M = ℝn,とおくと, I は G = M = ℝn 上の 対称な2項関係なので, ′ : 2G → 2M も ′ : 2M → 2G も 同じ操作になり, S ⊆ ℝn に対して
gIm ⇔ g⊥m
S ′ = {m∊ℝn | ∀g∊S; gIm} = {m∊ℝn | ∀g∊S; g⊥m} = S⊥であった. また, G = M と I の対称性より, BG = BM であることが解る.
BG = BM = {S⊥⊥ | S ⊆ ℝn} ⊆ Snである. 一方, H が線形部分空間のとき H = H⊥ だから,
Sn = {H | H は線形部分空間} = {H⊥⊥ | H は線形部分空間} ⊆ {H⊥⊥ | H ⊆ ℝn} = BG = BMである. 以上から, BG = BM = Sn.
H1 ∨ H2 = H1 + H2で, 例 7 より (BG, ⊆) における結びは
H1 ∨ H2 = (H1 ∪ H2)″ = (H1 ∪ H2)⊥⊥で与えられ, 今 BG = Sn であるから,
H1 + H2 = (H1 ∪ H2)⊥⊥であることが解る.

G = M = ℝn,(ただし,‹g,m› は g と m の内積) とおくと, I は G = M = ℝn 上の 対称な2項関係で, ′ : 2G → 2M も ′ : 2M → 2G も 極錐を取る操作 S ↦ S∗ になる. つまり, S ⊆ ℝn に対して
gIm ⇔ ‹g,m› ≤ 0
S ′ = {m∊ℝn | ∀g∊S; gIm} = {m∊ℝn | ∀g∊S; ‹g,m› ≤ 0} = S∗であった. このとき, BG = {S∗∗ | S ⊆ ℝn} (= BM) は, 閉凸錐の全体からなる族に一致する. 閉凸錐も極錐と同様に, 凸解析(非線形最適化などに用いられる分野)などに現れる重要な概念である.
