[開設 07/27/23]
例 3 の解説
ここでは,
n 次元 Euclid 空間 ℝn の線形部分空間全体からなる
半順序集合 (Sn, ⊆)
が束であることを示す.
資料「束」例 3 の
-
H1,
H2 ∊ Sn
に対して
-
H1 ∧ H2
=
H1 ∩ H2,
-
H1 ∨ H2
=
H1 + H2
≝
{x1+x2 | x1∊H1, x2∊H2}
(∧ と ∨ は (Sn, ⊆)
における交わりと結びの演算)を示す.
まず,
H1
と H2
が線形部分空間のとき,
H1 ∩ H2
と
H1 + H2
が線形部分空間になることは,
1 年次の「線形代数」で学んだと思う
(念のために ここ で説明している).
H1 ∧ H2
=
H1 ∩ H2
の説明.
(2ℝn, ⊆) において,
H1 ∩ H2
が {H1, H2} ⊆ 2ℝn
の最大下界であり,
(Sn, ⊆)
が (2ℝn, ⊆) の部分順序集合であることと,
(Sn, ⊆)
が共通集合の演算 ∩ に関して閉じていることから,
H1 ∩ H2
は {H1, H2} ⊆ Sn
の最大下界 H1 ∧ H2
である.
この説明がピンと来ない人のために,
丁寧な別の説明をしよう.
H1, H2 ∊ Sn
とする.
まず,共通集合の定義から
H1 ∩ H2 ⊆ H1
かつ H1 ∩ H2 ⊆ H2
なので,
H1 ∩ H2
は {H1, H2} の下界である.
次に,H ∊ Sn
を {H1, H2} の
任意の下界—すなわち H ⊆ H1
かつ H ⊆ H2
—とすると,
共通集合の定義から
H ⊆ H1 ∩ H2
である.
以上から,
H1 ∩ H2
は {H1, H2}
の (Sn, ⊆)
における最大下界,
すなわち H1 ∧ H2
=
H1 ∩ H2
となる.
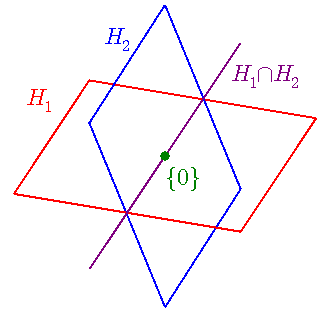
下限 H1 ∧ H2 のイメージ図
上図では H1 と H2 は ともに 2 次元線形部分空間,
それらの共通集合 H1 ∩ H2
は 1 次元線形部分空間.
{H1, H2}
の下界は H1 ∩ H2
と 0 次元線形部分空間 {0} だけであり,
下界全体の最大元は H1 ∩ H2 である.
H1 ∨ H2
=
H1 + H2
の説明.
任意の x1∊H1
に対して x1 = x1+0
∊ H1 + H2
だから,
包含関係の定義より H1 ⊆
H1 + H2
である.
同様に H2 ⊆
H1 + H2
なので,
H1 + H2
は {H1, H2} の上界である.
次に,H ∊ Sn
を {H1, H2} の任意の上界—すなわち,
H1 ⊆ H
かつ H2 ⊆ H
—とする.
任意の x ∊ H1 + H2
に対し,
H1 + H2
の定義から ある x1∊H1
と x2∊H2
が存在して x = x1+x2
となり,このとき x1∊H1 ⊆ H
かつ x2∊H2 ⊆ H
であって H が線形部分空間である
ことから x = x1+x2 ∊ H
となるので,
包含関係の定義より H1 + H2 ⊆ H
である.
以上から,
H1 + H2
は {H1, H2}
の (Sn, ⊆)
における最小上界,
すなわち H1 ∨ H2
=
H1 + H2
となる.
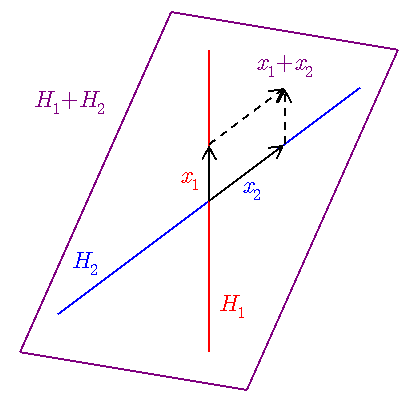
上限 H1 ∨ H2 のイメージ図
上図では H1 と H2 は ともに 1 次元線形部分空間.
それらを含む最小の線形部分空間は,
それらを含む 2 次元線形部分空間であり,
これは H1 + H2 である.
離散構造(室伏)のホーム




