[開設 07/31/23=MM/DD/YY]
概念束から文脈表と概念を求める
命題 4 の適用例
ハンドアウト掲載の概念束を例にとる.
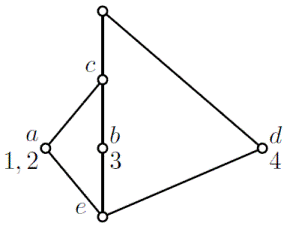
ハンドアウトにも書いたように,
図では記号 γ や μ は省略している.
つまり,
図中の 1, 2, 3, 4 は γ1, γ2, γ31, γ4 のことであり,
図中の a, b, c, d, e は μa,
μb, μc, μd, μe のことである.
命題 4 (i) γg ≤ μm ⇔ gIm
上図より
γ1 ≤ μa,
γ1 ≤ μc,
γ2 ≤ μa,
γ2 ≤ μc,
γ3 ≤ μb,
γ3 ≤ μc,
γ4 ≤ μd
なので,
命題 4 (i) より
1Ia,
1Ic,
2Ia,
2Ic,
3Ib,
3Ic,
4Id
となるから,
文脈表が
|
|
a
|
b
|
c
|
d
|
e
|
|
1
|
×
|
|
×
|
|
|
|
2
|
×
|
|
×
|
|
|
|
3
|
|
×
|
×
|
|
|
|
4
|
|
|
|
×
|
|
と復元できる.
命題 4 (ii)
A = {g ∊G | γg ≤ (A,B)},
B = {m ∊M | (A,B) ≤ μm}
命題 4 (ii) の意味するところは,
「その頂点以下の対象の全体が その頂点の外延であり,
その頂点以上の属性の全体が その頂点の内包である」ということである.
よって,
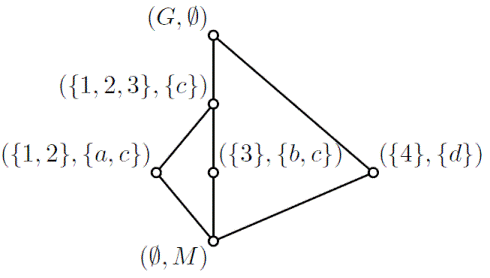
上図の各頂点の外延と内包は次のようになる.
|
頂点
|
外延
その頂点以下の対象全体
|
内包
その頂点以上の属性全体
|
|
最大元
|
{1, 2, 3, 4}
|
∅
|
|
c の点
|
{1, 2, 3}
|
{c}
|
|
|
{1, 2}
|
{a, c}
|
|
|
{3}
|
{b, c}
|
|
|
{4}
|
{d}
|
|
e の点
|
∅
|
{a, b, c, d, e}
|
これから,
ハンドアウト 3 ページ左下の図が
復元できる.
離散構造(室伏)のホーム



